 |
||
| . . . Chronicles . . . Topics . . . Repress . . . RSS . . . Loglist . . . | ||
|
|

|
 |
|||||
| . . . 2020-05-03 | ||||||
Diagrams are in a degree the accomplices of poetic metaphor. But they are a little less impertinent — it is always possible to seek solace in the mundane plotting of their thick lines — and more faithful: they can prolong themselves into an operation which keeps them from becoming worn out. [...] We could describe this as a technique of allusions.- Figuring Space (Les enjeux du mobile) by Gilles Châtelet
- Ancient and Modern Scottish Songs, Heroic Ballads, &c.,
collected and edited by David Herd, 1776 |
Peli Grietzer and I are separated by nationality, education, career, three decades, and most tastes.1 Our fellowship has been one of productive surprises (rather than, say, productive disputes). And when Peli began connecting machine deep-learning techniques to ambient aesthetic properties like "mood" and "vibe," the most unexpected of the productive surprises represented a commonality:
In relating the input-space points of a set’s manifold to points in the lower dimensional internal space of the manifold, an autoencoder’s model makes the fundamental distinction between phenomena and noumena that turns the input-space points of the manifold into a system’s range of visible states rather than a mere arbitrary set of phenomena.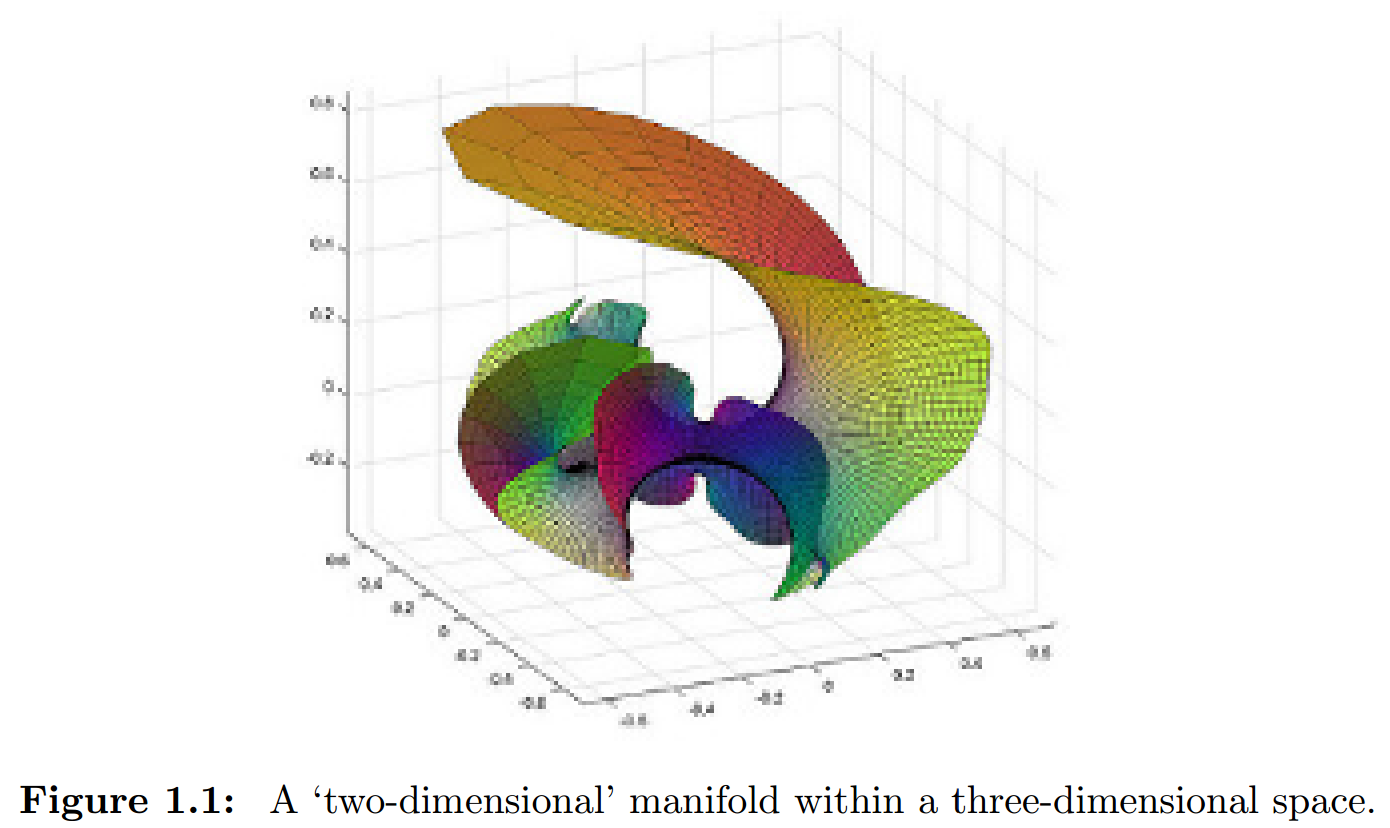
"A Theory of Vibe" by Peli Grietzer
(If Peli's sentence made absolutely no sense to you — and if you can spare some patience — have no fear; you're still in the right place.)
For two-thirds of my overextended life, I've carried a mnemonic "image" (to keep it short) with me. It manifested as a jerry-built platform from one train of thought to another, satisfactory for its purpose, and then kept satisfying as a reference point — or rather, to maintain its topological integrity, as a FAQ sheet. It guided practice and (if suitably annotated) warned against attractive fallacies. It didn't overpromise or intrude; it answered when called for. Over time it became mundane, self-evident, not worthy of comment. Although I've described its assumptions, its space, its justifications, and its uses, I never did quite feel the need to describe it.
My "image" had emerged from a very different place than Peli's, carrying a different trajectory and twisting out its own series of crumpled linens. What I felt in late 2017 was not so much the shock of recognition as the shudder of recognition with a difference: not a registration error to correct in the next printing so much as a 3-D comic which was missing its glasses. Still, though, recognizably "the same," as if Peli had passed by the smoke and noise of my informal essayism and assembled something resembling the ramshackle contraption which belched them out.
Encounters with an opinion or sentiment held in common always seem worthy of remark, being always scarce on the ground. But some remarks are worthier than others, and greeting years of hard labor with a terse "Oh yes, that old thing," like I was a crate of RED EYE CAPS or something, would be a dickhead move. And so there came upon me the happy thought, "Since Peli has shown his work, it's only fair for me to show mine."
1 Some divergences in taste might be artifacts of our temporal offset: William S. Burroughs and Alain Robbe-Grillet anticipated Kathy Acker and Gauss PDF about as closely as a low-budgeted teenager outside a major cultural center might have managed in the late 1970s, and my side of our most eccentric shared interest, John Cale,2 was firmly established by age nineteen.
2 "Moniefald," in this instance, being more or less synonymous with "Guts."
- "Psyche" by Samuel Taylor Coleridge
|
Over the following two-plus years I reluctantly came to realize that "showing my work" may have been an overambitious target: the work that went into that "image" consisted of my life from ages three to twenty-two; the work that's come out of that "image" contains most of my publications and most of what I hope to publish in the future.
That it is useless
Given the evidence of my résumé — a mathematics degree "from a good school," followed by 35 years of software development — you might think it friendlier of me to contribute to Grietzer's research program than to reminisce about my own. Which goes to show you can't trust résumés.
I programmed only to make a living, and every time I've tried to program for any other purpose, no matter how elevated, my soul has flatly refused. "We made a deal," my soul says. "A deal's a deal, man."
Anyway, I don't think the software side of things matters much except as conversation starter or morale booster. Computerized pattern-matching can be useful (and computerized pattern-generation can be entertaining) in their own right, but I'm in the camp who doubts any finite repeatable algorithmic process carries much explanatory power for animal experience, unless as existence disproof that an omnisciently divine watchmaker or omnipotently selfish gene are required.
As for mathematical labor, the work-behind-that-"image" includes the romantic history of my coupling with mathematics: meet-cute, fascinated hostility, assiduous wooing, a few years of cohabitation, and finally an amicable separation. I sometimes think of my "image" as a last snapshot of the old gang gathered round the table before we were split up by the draft and divorces and emigrations.
I haven't spoken to mathematics since 1982. Getting properly reacquainted would take as much effort as our first acquaintance, and, speaking frankly, if I live long enough with enough gumption to repursue any disciplined study, I'd prefer it be French.
I am, however, OK with bullshitting about mathematics, and have very happily been catching up on the past forty years of philosophy-'n'-foundations. Turns out a lot's happened since Hilbert! (Yeats studies, on the other hand, haven't budged.)
That it is trivial
As mentioned above, I never felt a need to describe my "image," much less ask who else had seen it. Once I started looking, the World Wide Concordance easily found some pseudo-progenitors and fellow-travelers. Maybe my exciting personal discovery was something which virtually everyone else on earth already had, unspoken, under their belts, like masturbation, and my reaction to Grietzer's dissertation was a case of "shocked him to find in the outer world a trace of what he had deemed till then a brutish and individual malady of his own mind."
That it is redundant
Also as mentioned above, I've touched or traversed some of this ground before, and came near as dammit to sketching the "image" itself in a summary of development and beliefs which still pleases me by its concision. And here I sketched the transition from positivist analytic philosophy to pragmatic pluralism; there I described the heady combination of Kant and acid; a bit later I wrote all I probably need to write about aptitude and career....
Much of my dithering over this present venture comes down to fear that I'm taking a job which has already been perfectly adequately done, and redoing it as a bloated failure. God knows there are precedents.
That it is
There are two senses of "showing the work" in mathematics. What's typically published is a (proposed) proof, an Arthur-Murray-Dance-Studios diagram which indicates (one hopes) how to step down a stream of discourse from (purportedly) stable stone to stable stone until we've reached our agreed-upon picnic spot.
But closer to the flesh, very different sorts of choreography come into play. For the working mathematician, what impels and shapes the proof is the work of observation, intuition, exploration, and experimentation. For the teacher (depending on the teacher), tutor, or study group, the proof is meaningless without a motivating context and a sense of the mathematical objects being "handled," and those can only be conveyed by implication — by descriptions, metaphors, examples, images, gestures, and applications:
It is true, as you say, that mathematical concepts are defined by relational systems. But it would be an error to identify the items with the relational systems that are used to define them. I can define the triangle in many ways; however, no definition of the triangle is the same as the “item” triangle. There are many ways of defining the real line, but all these definitions define something else, something that is nevertheless distinct from the relations that are used in order to define it, and which is endowed with an identity of its own.We disagree with your statement that the ideal form of knowledge in theoretical mathematics is the theorem (and its proof). What we believe to be true is that the theorem (and its proof) is the ideal form of presentation of mathematics. It is, in our opinion, incorrect to identify the manner of presentation of mathematics with mathematics itself.
- Indiscrete Thoughts by Gian-Carlo Rota
But what are we studying when we are doing mathematics?A possible answer is this: we are studying ideas which can be handled as if they were real things. (P. Davis and R. Hersh call them “mental objects with reproducible properties”).
Each such idea must be rigid enough in order to keep its shape in any context it might be used. At the same time, each such idea must have a rich potential of making connections with other mathematical ideas. When an initial complex of ideas is formed (historically, or pedagogically), connections between them may acquire the status of mathematical objects as well, thus forming the first level of a great hierarchy of abstractions.
At the very base of this hierarchy are mental images of things themselves and ways of manipulating them.
"Mathematical Knowledge: Internal, Social and Cultural Aspects"
by Yu. I. Manin
Similarly, to justify a text a motivated Author is desired; if none is found, religious and literary histories prove that one will be invented. A legislature inscribes laws, but those statutes are meaningless gibble-gabble without politics to justify them and enforcement to materialize them. And hoity-toity structuralist though I am, I confess I gained more from classic philosophy texts after I began reading them as abstract self-portraits.
Something outside the proof, the text, or the statute — and possibly even something outside my cheerfully concise spiritual C.V. — is needed to derive a "real" (that is, "perceived"; that is, "dimensioned") object from what would otherwise be just another segment of a one-dimensional droning continuum — or be even less than that.
To use an image I've used before and will use again, we need to put skin on that game and meat on those bones:
When two proofs prove the same proposition it is possible to imagine circumstances in which the whole surrounding connecting these proofs fell away, so that they stood naked and alone, and there were no cause to say that they had a common point, proved the same proposition.One has only to imagine the proofs without the organism of applications which envelopes and connects the two of them: as it were stark naked. (Like two bones separated from the surrounding manifold context of the organism; in which alone we are accustomed to think of them.)
- Remarks on the Foundations of Mathematics by Ludwig Wittgenstein,
third revised edition
A manifold, in general, refers to any set of points that can be mapped with a coordinate system. [...] In the context of autoencoders, one traditionally uses ‘manifold’ in a more narrow sense, to mean a lower-dimensional submanifold: a shape such that we can determine relative directions on said shape, quite apart from directions relative to the larger space that contains it. From the ‘internal’ point of view—the point of view relative to the manifold—the manifold in the illustration is a two-dimensional space, and every point on the manifold can be specified using two coordinates. From the external point of view—the point of view relative to the three-dimensional space—the manifold in the illustration is a ribbon-like shape curling hither and thither in a three-dimensional space, and every point on the manifold can only be specified using three coordinates.
Ambient Meaning: Mood, Vibe, System by Peli Grietzer
The wolf comes down on the fold; I place a three-fold napkin beside my plate; when we host four guests, we need threefold napkins; when playing poker I either fold early or lose my bankroll.
Given working knowledge of the words many and fold, most usages of "manifold" are fairly easy to decipher:
The apparent exception is mathematics, where the most commonly encountered definition is something along the lines of "a topological space each point of which has a neighborhood homeomorphic to a Euclidean space."
And this isn't just a case of English being led astray, like our settling on computer when the French wisely held out for ordinateur: mathematical-French for manifold is the nearly synonymous variété.
A look at the source which both words were translating clarifies things a bit.
Riemann was more ambitious. He also wanted to generalize Euclidean geometry to handle variable properties other than the familiar height-width-depth of physical space: color or mass, for example. And he wanted to generalize those familiar spatial coordinates to allow for the possibility of other geometries — notably the possibility of a globally non-Euclidean curved physical space, unbounded but finite, similar to the globally non-Euclidean physical surface of the Earth.
To describe those generalizations, Riemann needed words other than "surface" and "space". (As a popularizer of Riemann's ideas told an outraged conservative who accused him of trying "to spread and support the views of the metaphysical school," "The 'manifold' I described in my paper is not a space.") And because his generalization involved a whatsit whose "interior" could be minimally plotted by one or more varying properties, and whose "exterior" could be minimally described by adding one more varying property, he settled on Mannigfaltigkeit. His paper also tries out "n-fold extent" and "n-fold continuum" and "n-ply extended magnitude," but "manifoldness" and "manifold" were less overloaded terms, and so "n-dimensional manifold" won out in the research and textbooks that followed.
Our present-day topological manifold specifies that each point exist in some "neighborhood" of other points, so that the manifold can be treated (locally) like a sub-surface or a sub-space of its own. Riemann's original definition was broader. Because he asked only that the specified things be distinguished by quantifiable properties, his manifoldnesses included collections of widely scattered individuals, no matter how unneighborly they might be:
According as there exists among these specialisations [i.e., instances of the general collection] a continuous path from one to another or not, they form a continuous or discrete manifoldness; the individual specialisations are called in the first case points, in the second case elements, of the manifoldness. Their comparison with regard to quantity is accomplished in the case of discrete magnitudes by counting, in the case of continuous magnitudes by measuring.Although "discrete manifolds" didn't make it into topology, Riemann's rationale for including them still holds interest for myself and Grietzer, I think.
When learning German I had a lot of false-friend interference from Spanish, such that I kept interpreting "mannigfaltig" as "not enough people."
| . . . 2020-05-05 |

In this paper, I will picture
I will illustrate a law.
Everybody likes to picture;
No one wants to learn to draw.
Imagine that the graph-paper-covered room above is a warehouse (offsite storage for a museum or a library, say, or a barn) completely filled by some sort of object or another (archaeological artifacts; books; fodder), piled up and shoved back in some order that I'll leave vague for now.
And now imagine all the warehoused objects of some more specific sort (pseudo-red-figure painting; cyberpunk novels; mycotoxin-contaminated grains) hovering on or near that twisted and tugged tie-died sheet like mosquitoes attacking a net. Then (if we really wanted to) we might say to ourselves that the sheet represents the subcategory.
As to why anyone would really want to say such a thing — well, I'll get to that too. First, though, I should confess that the figure I've been pointing to is randomly chosen clip-art, and the reassuringly regular digits marked off along its edges have sweet fuck-all to do with what I've been asking you to imagine. I placed the image there as an arbitrary sample of an allegorical simplification (reduction to three Euclidean dimensions from an indefinitely expanding set of "real" dimensions, some of which are discrete and finite, others continuous and infinite, others difficult to describe at all) of an inexact metaphor for some concepts of interest to myself and Dr. Grietzer.
For both of us, what's imaged is the launch of a research program rather than a graphic summary of its conclusion.
I wonder to what degree doing mathematics is constructing a mental model for a mathematical object, comparing the properties of that model to the facts associated to the object and then trying to reconcile the model with the facts?Jon Bannon at MathOverflow
Revisiting my randomly chosen absurdly oversimplified allegorical diagram, let's say our warehouse is full of digitized photographs and we're interested in those which contain smiling faces (whether lying or not). Where might they be found?
That depends on how the warehouse contents were originally sorted, or, equivalently, what the fictional coordinates marked off on those imaginary walls might be measuring.
Say left-to-right marks the brightness of the top-leftmost pixel of a photograph, back-to-front marks the color of the bottom-rightmost pixel, and floor-to-ceiling marks the original photograph's area in millimeters. Then the photos we want would probably look as if they were shoved into the warehouse at random.
Which doesn't necessarily mean that they'd look random in our imaginary diagram of the warehouse. If the warehouse contained only 3.5" x 4.25" Polaroids, then smiling-faces would be graphed as points in one satisfyingly compact little sphere. But we wouldn't have learned much, since all the uninteresting photographs would be there too.
And so my and Grietzer's "image" contains the implicit assumption that we can collect some dimensions which are germane to the subcategory of interest: some things other than the categorization itself which could (after a brisk massage) help distinguish the interesting objects from their neighbors. That assumption might be wrong. Given a warehouse of Polaroids and nothing else, there might simply be no distinguishable-or-distinguishing pattern for the immunization records (or criminal inclinations, or IQs) of those depicted no matter how many measurable dimensions we throw at the problem.
One must anyway admit that a question need not have answers, that it is not even bound to have any, since a great part of scientific activity consists, precisely, in seeking the good questions. Thus, the correspondence between planets and regular polyhedra, of which Kepler was so proud, is not even a wrong hypothesis, it is an absurd connection, which only deserves a shrug of the shoulders, a question that did not deserve to be posed, to be compared to speculations linking the length of a ship with the age of her captain. Transparency stumbles on the questioning as to the interest of questions, next on the difficulty to find the answers to the supposedly good problems. Indeed, answers are, mostly, partial: a half-answer accompanied with a new question. The relation question/answer thus becomes an endless dialogue, an explicitation process; it is in this process, which yields no definitive and totalising key, where the afterworld of appearances, i.e., knowledge, is to be found.- The Blind Spot: Lectures on Logic by Jean-Yves Girard
Besides the dimensions tick-marked across the warehouse edges, both Grietzer's trained-autoencoder "image" and my self-generated "image" hide another dimension in plain sight: the dimension which measures if (or how much) a particular thingmabob matches the particular category of interest:
"This is a face. And this is a face. No, that's not a face. But this here is a face."
"Is this a face?"
"Sort of, I guess; it's a dog's face."
"Are these dog's faces?"
"No. Willie and Joe are dogfaces, but what they have are real faces."
If the question is "How close is that particular thing to what we mean by this name?", then what the manifold depicts is "What we mean by the name." And unless "What we mean by the name" is well and stably agreed upon, we can't expect to derive well and stably agreed upon results.
For categories like "Smiling Faces," that caveat is easily ignorable, albeit at the risk of it publicly biting you in the ass after you've trumpeted your success. But tribal and cultural labels (ethnicity, religion, nation, discipline, art, genre) are blatantly impermanent and localized. They appear post-facto, they vary by time and place, they pass away, and their applications are disputed throughout their existence.
"Nostalgic music," for example, is an easily explained category which can't be placed by sonic properties alone. The germane dimensions are observer-dependent: age and circumstances of the first encounter; extent of later encounters.... For American sports fans, "The Star-Spangled Banner" is unlikely to be nostalgic, whereas their high-school marching band's fight song might be.
Artistic genres, on the other hand, are socially negotiated but also socially contested, and their rival imaginary-manifolds will be involuted, trimmed, and extended (science fiction incorporating alternate history; romances incorporating the undead) until the genre becomes moribund.
Here was my initial random snatch of a computer-generated image:

And here is another piece of sample-allegorical clip art, grabbed from an introduction to autoencoding techniques in Python (and thank you, Jake VanderPlas):
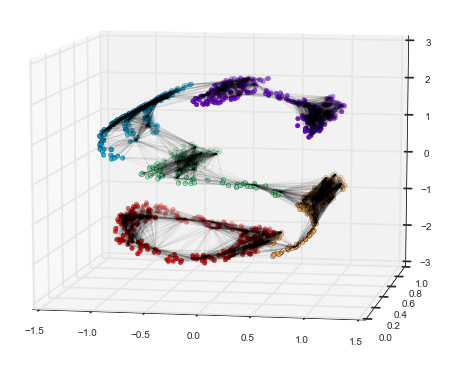
Considered purely as suggestive fact-free allegory, the first figure has a more or less arbitrary look, like a satellite photo of a landscape generated and weathered by unpredictable forces, or a spectacularly unmade bed, or a smushed hunk of clay. "It is what it is," but could easily be something different. Contingent, it invites further contingency.
The second figure suggests a definite thing-in-itself, with its own integrity, crystallized or grown or manufactured, hidden by noise and then unearthed.
A picture is worth a thousand words, most of which disagree. My own "image" stands in for a baggy one-size-fits-all Emperor's-New-Clothes sort of allegory, a fluffy cloud bobbing in hot air.
Whereas the extended legend attached to Grietzer's chart points toward some more, well, pointable things — up here an intuited "vibe" or "feel" or "groove" shared by representatives of this set of artifacts — and down there some machine learning techniques whose usefulness largely depends on the extent to which distinctive latent features can be derived from the set. (Any random selection of UTF-8 transcriptions of European texts, for example, can support some sort of autoencoding, but the "latent features" will probably approximate an equally random list of suffixes, prefixes, and roots.)
Because criticism must articulate a system of differentials- "Shall These Bones Live?" by Jerome J. McGann
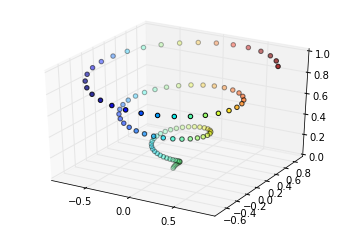
If we (virtually) reach into the previous graph, take that enticingly physical-looking ribbon, give both ends a good yank, and flatten it out, we can read a TOP SEKRIT MESAJ:
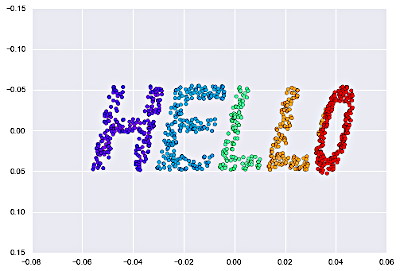
What machine-learning usefully "learned" in this case wasn't so much an ability to spot new category matches in the original three-dimensional space, as it was something about the arrangement of matches across the derived two-dimensional manifold itself. (Our deft jerk, however, discarded the original graph's equally readable "S", and so perhaps we'd better keep the higher-dimensional affair around.)
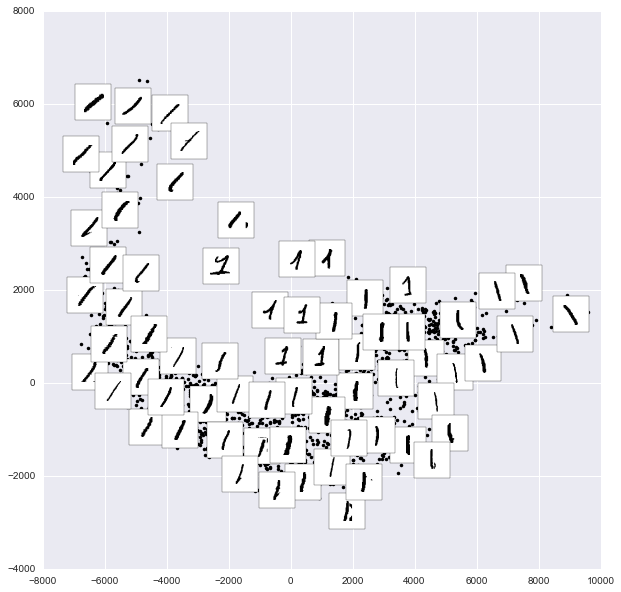
More generally, where autoencoder compression might help human interpreters find latent features, manifold visualizations might help expose latent dimensions. VanderPlas's much-plundered page shows how arranging sample images of handwritten digits over their positions in the derived manifold calls out variations in slant, the choice of serif or sans-, and noisy bits we might want to correct somehow:
Elsewhere on that page, a manifold arranges a rogue's gallery of faces to pivot from left-profile at the top through full-face to right-profile at the bottom.1
And elsewhere in Grietzer's verbal explorations of his "image":
[...] no less than it means a capacity to judge whether a set of objects or phenomena does or does not collectively possess a given style, to grasp a ‘style’ or ‘vibe’ should mean a capacity to judge the difference between two (style-conforming) objects in relation to its framework. Learning to sense a system, and learning to sense in relation to a system—learning to see a style, and learning to see in relation to a style—are, autoencoders or no autoencoders, more or less one and the same thing.
1 Those overlapping playbills irresistibly recall the attempt to flatten a projection of my scattered wits against dorm room walls: a full-page tabloid photo of three rednecks preening en route to crack skulls at a civil rights march; my father's "Please, Mr. President, Don't Go!" petition from the John Birch Society; Patti Smith cupping her bare breast; Samuel R. Delany's sultry Tides of Lust author photo; beatific Squeaky Fromme led to prison; Bobby London's Ramones portrait; the Eraserhead poster as memento-mori of my summer-long St. Louis nightmare; M. K. Brown's perky "Magic Orange"; the white rat's funeral from Khatru 6; naturally-wavy-haired Yeats defocusing for the camera....
The SHELLO graph's origin page describes the effort of its unearthing:
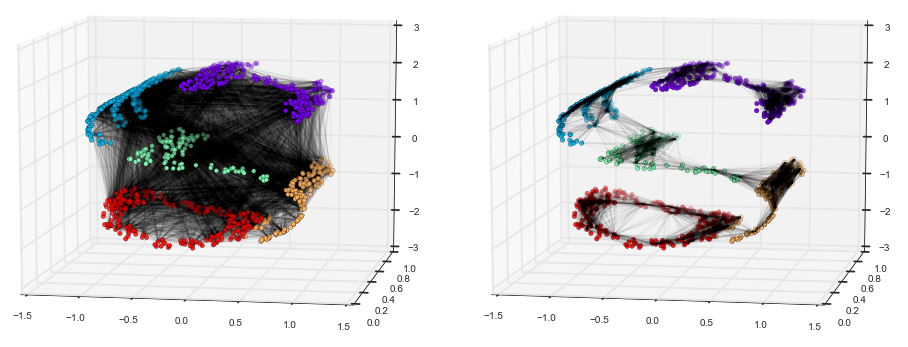
The left-hand picture was generated by one algorithm for summarizing the distance between points; the right-hand picture was generated by a different algorithm.
As I established early in my research career via a series of rigorously fucked-up connect-the-dot trials by crayon, any fixed set of points can be plotted onto an unlimited choice of surfaces. How do we choose? Why should we choose?
For typical machine learning applications, we're after a submanifold that not only connects or closely neighbors our original dots, but will also encompass or approach previously uninspected points of the "same type" or "same border between types," so that new specimens can be classified, denoised, or generated.
But what if we don't want a typical machine learning application? If we aren't interested in improving the product recommendations Amazon shows to collectors of Kathy Acker, or in generating Trump re-election ads in the style of "Eumaeus" for Facebook? (I mean, I've already read books which manually approximate what Google's DeepDream would output if it had trained on Kathy Acker or Thomas Bernhard instead of dog faces, and I'm not sure they were worth the effort.) What if we don't actually expect to glance at a machine-quilted Scholar's Counterpane of modernist texts and see one axis of parataxis-to-cohesion crossed by another axis of working-class to upper-crust? In that case why shouldn't we rest content, be grateful for the nice tidy plateful of points we've been dished, and leave it at that? What do we think we're doing?
A possible answer is this: we are handling real things which can be studied as if they were ideas, "reproducible objects with mental properties." Each such object must be rigid enough to keep its shape in any context it might be used. At the same time, each such object must have a rich potential of making connections with other objects, and the connections between them may acquire the status of ideas as well.
"When any man pretends to mix in manifold activity or manifold enjoyment, he must also be enabled, as it were, to make his organs manifold, and independent of each other. [...] How difficult, though it seems so easy, is it to contemplate a noble disposition, a fine picture, simply in and for itself; to watch the music for the music's sake; to admire the actor in the actor; to take pleasure in a building for its own peculiar harmony and durability. Most men are wont to treat a work of art, though fixed and done, as if it were a piece of soft clay. The hard and polished marble is again to mould itself, the firm-walled edifice is to contract or to expand itself, according as their inclinations, sentiments, and whims may dictate: the picture is to be instructive, the play to make us better,— every thing is to do all. The reason is, that most men are themselves uninformed, they cannot give themselves and their being any certain shape; and thus they strive to take from other things their proper shape, that all they have to do with may be loose and wavering like themselves."- Wilhelm Meister's apprenticeship and travels,
translated from the German of Goethe by Thomas Carlyle
Returning to Jake VanderPlas's SHELLO graphic:

Rather than silently translating that crudely material vehicle into mathematical objects consisting of naught but coordinates, let's take the definitely more-than-none pixels on the screen (or more-than-none inked areas on the page) at their graphic word, and reconsider those imaginary zero-dimensional points as bounded neighborhoods (or submanifolds) of their own, multi-dimensional spaces which maintain their own integrity. (If the sample data consists of books, or movies, or paintings, or, for that matter, human beings, this will, I hope, not seem counterintuitive.)
Then the manifold vectors which previously connected-the-dots now pierce-the-objects. If the categorical manifold changes shape, its intersecting vectors shift like a flashlight playing around the object's interior.
At which the categorizing submanifold stops being a destination place and starts to become an interpretative filter. We may decide to switch goals and gears, so that our so-to-speak job is no longer to tighten and stabilize the focus of an embedding submanifold, but instead to transform an exploratory submanifold. We might do so by adding or removing or re-weighting the data's input dimensions — the extent to which it justifies the divine right of kings, for example, or the correctness of its diction — or we might instead radically change our training-set of sample data — by adding, for example, a notoriously unsuccessful attempt at rollicking sea adventure to the canon of nineteenth-century American literature.
More particularly, I might do so. Not to establish a more solid representation of a canon, but to trace through a space, to cast a new (or at least new to me) light, to burn with, if not — god no — not a "diamond-like flame," possibly not even a disco-ball-like flame, at least a lava-lamp-like flame.
When Bernhard Riemann introduced "manifoldness" into mathematics, he did so hoping to liberate physicists from Kantian constraints on the imaginable Real. Then, rather than presuming that the a priori notions of continuous and infinite Euclidean geometry always and necessarily described space-that-is-the-case, scientists could (and must) let their models be guided by physical observation. As one example, it might be that three-dimensional Euclidean models were only more-or-less-effective over relatively small distances, and that if scientists were able to zoom out enough, they'd find something more like the non-Euclidean surface of the Earth: curved and finite.
Turning from imaginary telescope to imaginary microscope, Riemann suggested that real-world space wasn't necessarily infinitely dividable; it might merely be parceled out in packets too small for us to notice. Which (he wrote) carries some interesting consequences:
In this respect there is a real distinction between mere extensive relations, and measure-relations; in so far as in the former, where the possible cases form a discrete manifoldness, the declarations of experience are indeed not quite certain, but still not inaccurate; while in the latter, where the possible cases form a continuous manifoldness, every determination from experience remains always inaccurate: be the probability ever so great that it is nearly exact. [...] Now it seems that the empirical notions on which the metrical determinations of space are founded, the notion of a solid body and of a ray of light, cease to be valid for the infinitely small. We are therefore quite at liberty to suppose that the metric relations of space in the infinitely small do not conform to the hypotheses of geometry; and we ought in fact to suppose it, if we can thereby obtain a simpler explanation of phenomena.[...] in a discrete manifoldness, the ground of its metric relations is given in the notion of it, while in a continuous manifoldness, this ground must come from outside. Either therefore the reality which underlies space must form a discrete manifoldness, or we must seek the ground of its metric relations outside it, in binding forces which act upon it.
Closer to virtual-home, if for argument's sake (and certainly nothing else is at stake) we assume that all possible purely-textual works can be contained in sets of 1-to-4000 page volumes containing 32-bit Unicode characters, then the Universal Library is clearly finite. Too large to fit on my phone's SD card, maybe, but still of calculable size. And although it'll sadly lack Krazy Kat, Sherlock Jr., and Never Buy Texas from a Cowboy, there's nothing to stop our constructing a similarly finite Universal Spotify of 0-to-100-dB 1-to-64800-seconds 24-bit FLAC files, then moving on to a finite Universal Coffee-Table of art prints, and a finite Universal Movie Archive....
As Riemann wrote, and as the Universal Comedy Club independently discovered, if you want to find an element in a discrete manifold, you don't need to fuss with never-completely-accurate comparative measurements: you can just count off the elements and assign each an index number for precise future reference. But then you need some way to remember that Joke 847656 requires a Yiddish accent, and Joke 57 is not for mixed company, and Joke 766362254 might be too soon, too soon, and at some point it's easier to just try to re-tell a joke.
We assembled a loverly bunch of signifiers, and several data server farms of signified objects, but we bottlenecked on interpretants. Although our collection may be discrete and finite, since each reader will encounter different subsets of the collection in different orders at different times in the midst of different contexts, no Reading Experience will be repeated and the Conversation will remain, if not Infinite (unlikely, given the fragile set of conditions required for any Reading Experience to exist at all), then at least Interminable within reach of the Library. Of taking many books there is no end.
The Universal Library demonstrates that our sense of culture's infinite dimensionality, of an unbounded continuous manifold, must derive from something other than a (relatively) small number of artifactual points. Conversely, if we lean in more closely, those artifacts no longer look so pointy. When we actually open one of the volumes which seem so impressively solid on our shelves (organized as they are by binding size and color), we find hundreds of dark smears on yellowing paper, and then another big bunch of dark smears, and another, and another — where the hell did the book go?
Just as there's eventually some audio sampling rate at which a strictly finite digitization becomes humanly indistinguishable from an analog sound even if the human is Neil Young, it's possible that the apparent continuum of space-time comes in strictly indivisible packets. Since humanity (like other animals) remains incapable of holding all of those digital samples or all those space-time packets separately in mind, human experience will remain analog and continuous and simpler: we will read one extended book and hear one extended sound and see one extended object.
Again as pointed out by Riemann, once you've committed to the quantitative simplicity of continuity (one persistent physical thing with a heft and a surface texture, instead of umptygazillions of vectors of probabilities seeping and spraying every which where and when), you've also condemned yourself to imprecision. We're never gonna get it right.
Which is good. Rightness isn't what we've been built for; we'd never have time to get anything done. Giuseppe Longo straightforwardly founds our a priori (or so) ideas of the infinitely extensible horizon and the infinitely divisible continuum on mammalian forgetfulness and boredom, and I don't see why we'd need anything more hifalutin. Our cognitive limitations are effective adaptations to Real Life.
In turn we use those cognitive limitations as cognitive tools: they make movies move, make a novel out of graphical variations, make a song out of amplitude samples, and make a geometry out of give-or-take or just-plain-wrong measurements. And we then use those imprecisely derived exactitudes to construct new and occasionally useful imprecisions: a physics,1 a faith, a revised physics, a reformed faith....
1 Clumsy conscience-haunted easily-distracted students fare poorly in labs. Listening to a podcast during one of my last commutes, I felt a keen fraternal warmth towards Carol Cleland:
I was a physics major, but I didn’t like labs. I was a klutz in the lab and my experiments never turned out right, and I was more interested in theoretical science. [...] I was always the last one; something was always wrong with my equipment. Just like when I cook. When I cook and I follow a recipe, I never come out with the same thing twice. [...] I'm not really good at following procedures.
On the considerably smaller scale of Grietzer and myself, our (apparently) graspable "image" takes the place of something which cannot be itself be fully articulated: an attractive ambient feeling which seems to be shared across a set of artworks, or a sheaf of possible connections between experiences-of-the-real and objects-in-the-world. We share an impulse to describe a neighborhood around or within each not-so-atomic atom.
Alternatively, we could steal a trick from Riemann's quanta and WAV's amplitude slices and try to make the invisible and/or imaginary manifold irresistibly apparent even without connectives. If we arrange our canonical samples closely enough and selectively enough, we don't necessary have to draw the lines or drape the sheet ourselves:
And this may be one spot where our preferred methodologies overlap. I'm clearly attached to collage and found-writing, both as consumer and as so-to-speak "producer". (I often feel I "produce" nothing else.)
As for Grietzer:
This relates to what I’m really excited about, which is undoing the distinction between ‘interpretation’ and ‘erotics’ (in the Sontag sense) or between ‘cognitive mapping’ and ‘listing’ (which Jameson is fixated on), or between mimesis on the one hand and curation, installation, and collage on the other. The fundamental drive is really to create a viewpoint where the ‘radically aesthetic’ — art as pure immanent form and artifice and so on — is also very, very epistemic.- “‘Theory of Vibe’: A conversation with Peli Grietzer” by Brian Ng
Should we call such a move creation or interpretation or simple parasitism? That question is above my pay grade but I'm fairly comfortable with calling it a construction.
The question of motive remains. Even if we do manage to find some subset of the population who are able to see the ducky or horsie we've so carefully assembled, what would compel us to act out in such an eccentric manner? What's the parasite get out of it?
I'll attempt an answer in this saga's third volume, a thrilling tale of love, literacy, and mathematics. (For my neighbors' peace of mind I'll go light on love.)
But first an end-point.
- Parmenides, as translated by Shaul Tor
in Mortal and Divine in Early Greek Epistemology |
Heaven and earth are equipped with a set of kiln-bellows and air-pipes. Once the mechanism starts moving, wherever the moving air reaches all is stirred. To the ignorant this is the acme of mechanical genius, but what do the pipes and bellows do? They remain void without collapsing. That is why they can move again and continue producing. And so ten thousand things are created, the manifold forms etched and carved between the heavens and the earth. Those who see the heavens and the earth producing fail to realize that their productivity depends on their emptiness.- Su Che, quoted in Dao de jing: the book of the way, translation by Moss Roberts
There would be nothing whatsoever that was to be done, action would be uncommenced,
and the agent would not act, should emptiness be denied.
The world would be unproduced, unceased, and unchangeable,
it would be devoid of its manifold appearances, if there were intrinsic nature.- Nāgārjuna’s Middle way: the Mūlamadhyamakakārikā,
translation by Mark Siderits and Shōryū Katsura
- "Bidding the Moon" by James Stephens
|
Like Belgium, the island of Parmenidea brings two nations into uneasy proximity: Aletheia (that's pronounced "Althea") and Doxia.
Aletheia, "Land of Abstractions," promises investors immortal, unchanging, unyielding, and singular Truth, by which, so far as I've been able to ascertain, is meant perpetual warfare. This is my own, my native land. However, the fatherland didn't conveniently border a plannedparenthoodland, and I've always gotten the impression that it would sort of prefer to see me dead. (I'm not saying that's necessarily bad, mind you; I'm just saying.)
Doxia, "World of Meat" (or, as Aletheians prefer to call it, "World of Hurt") promises only transient Reality (or, as Alethians prefer to call it, "the conventionally real").
My fellow Aletheians are correct (correctness is their business!) in accusing Doxia of a surfeit of suffering. They less frequently mention the liberality of our own pours. Doxia may not exactly be the land of milk and honey — that would be seismically unsound even by mundane standards — but it is the land with some occasional milk and honey. A taste: worse or better than none at all?
Down the road a piece, the roulette wheel at Pascal's Casino offers a choice between thirty-six slots (Jansenist, Lutheran, Sunni, Shi'ite, Zoroastrian, Shaktist, and so on and on and on, but let's stop at thirty-six), each of which promises eternal joy for you and eternal agony for the rest of the table if it pays off, and a final thirty-seventh (the green zero) which pays a teaspoon of honey and lifespan-limited suffering all round. It is, obvs, a matter of taste, but I'd feel like an ingrate if I placed my wager elsewhere.
Thus am I a traitor to my country as well as my class. Unfortunately, I retain too strong an accent to ever feel fully at home in Doxia, or be welcomed as a native. And so, in my touristic wannabe way, I approximate as best I can that happy land fur, fur away (yet as near as the kiss of a brick) with the one language I've been given.
But trying to directly communicate the space of all possible communications, the indefinitely-dimensional real continuum itself, is literally pointless. Instead of inducing synesthesia, we create a tsunami of noise: the medium becomes opaque, a wall. Reading Finnegans Wake aloud clarifies it only by forcing us to select a through line ("Oh, I see, this is really 'God Save the King'"), temporarily defocusing everything else into ambient atmosphere or chicken fat. The fish can't describe water but the fish can traverse it.
Why a "manifold" rather than "scattered points in a multidimensional space whose axes are chosen to draw them closer together"? Or a "named finite set of elements"?
My goal (like most worthwhile goals, only describable once you've decided you've reached it) was to replace (as best I could) the ugly choice between anguished conflict and pratfalling certainty by that "pleasant confusion which we know exists." In a pleasingly confusing paradox, that goal is as one with what Giuseppe Longo calls "knowledge construction" (which "will obviously replace, in mathematics and in natural science, the notion of 'ontological truth'") and Fernando Zalamea calls mathematic vision:
To those ends, we will adopt certain minimal epistemological guidelines, furnished in philosophy by Peirce's pragmatism, and in mathematics, by category theory.A vision moderately congruent with the multiformity of the world should integrate at least three orders of approximations: a diagrammatic level (schematic and reticular) where the skeletons of the many correlations between phenomena are sketched out; a modal level (gradual and mixed) where the relational skeletons acquire the various 'hues' of time, place and interpretation; and a frontier level (continuous) where webs and mixtures are progressively combined. In this 'architecture' of vision, the levels are never fixed or completely determined; various contextual saturations (in Lautman's sense) articulate themselves here (since something mixed and saturated on a given level may be seen as skeletal and in the process of saturation in another, more complex context) and a dynamic frontier of knowledge reflects the undulating frontier of the world.
[...] One obvious obstruction is the impossibility of such a system's being stable and definitive, since no given perspective can capture all the rest. For, from a logical point of view, whenever a system observes itself (a necessary operation if it seeks to capture the 'whole' that includes it), it unleashes a self-referential dynamic that ceaselessly hierarchizes the universe. As such, a pragmatic architectonic of vision can only be asymptotic, in a very specific sense interlacing evolution, approximation and convergence, but without a possibly nonexistent limit. An 'internal' accumulation of neighborhoods can indicate an orientation without having to invoke an 'external' entity that would represent a supposed 'end point' - it has the power to orient ourselves within the relative without needing to have recourse to the absolute.
- Synthetic Philosophy of Contemporary Mathematics by Fernando Zalamea
Can these words be made flesh? These wooden bones of abstraction become a Real Live Boy? No, but they more closely approach that unbroachable phase shift with gesture, the sweep of articulation through space and time, miming the thick dimensionality of organic form through transforms and translations which, if nothing else, can proudly lay claim to mortality.
| . . . before . . . | . . . after . . . |
Copyright to contributed work and quoted correspondence remains with the original authors.
Public domain work remains in the public domain.
All other material: Copyright 2020 Ray Davis.