 |
||
| . . . Chronicles . . . Topics . . . Repress . . . RSS . . . Loglist . . . | ||
|
|
|||||
| . . . Badiou | |||||
| . . . 2003-07-03 |
The Ultimate Battle Between Good and Nice
I throw around the word "evil" a lot. I come from a small midwestern town, so the concept feels comfortably familiar. Familial, even.
Evil is grudges and pariahs and book-banning and hellfire, lynching and sniping, righteous greed and willful ignorance. It's chopping and deforming and squeezing experience into a single-P.O.V. heroic narrative learned from soap opera or sports or lives of the poets. It's clinging to (or even manufacturing) the "kinds of circumstances" in which we need feel no qualms about cowardly cruelties ranging from deliberate public insult to mass murder. Oh, and whoever bred those little pug dogs that can't breathe comfortably or retract their tongues? It's that guy too.
In short, evil is the refusal to deal with particulars.
Alain Badiou says that evil isn't self-evident. Still, he seems pretty certain of himself: good is rigidity and evil is anything that might make you re-examine your premises, or even let other people sleep there overnight. Good is universal condemnation; evil is the notion of individual variation. Good is a focus on extreme circumstances that permit the indulgence of extreme measures.
Thus Lenin and Mao (and presumably Stalin and Kim Jong Il) are good. "The ethics of Truth always returns, in precise circumstances, to fighting for the True against the four fundamental forms of Evil: obscurantism, commercial academicism, the politics of profit and inequality, and sexual barbarism."
Not that I've met Badiou, or want to, but having met evil several times a day for most of my life, it'd be rude to pretend I don't recognize its face.
"The Good in artistic action is the invention of new forms that convey the [fixed] meaning of the world. The Good in science is the audacity of free thought, the joy of exact knowledge."Me, I'd say the good in art is what gives pleasure and the good in science is what approximates reality. Insofar as we derive pleasure from proximity to reality, there's some ambiguity there, but I think my art and my science are easily distinguished from Badiou's.
As for my politics, if he's right that my choice is Bush or Lenin, neither of whom were democratically elected in the first place, I'll just stay here in the basement till they smoke me out.
Luckily, Badiou's oppositions tend toward the superficial. (Like, just who should declare war on whom to save the "projected ten million dead from AIDS in Africa"? War doesn't have a great record as an antiviral agent.) To "take the nearest example," Bush wasn't in the WTC when it went down, but some of his enemies were, and the hijackers were led by relatives of his business associates. Given that, is it really safe to say "Bush is evil, therefore Osama is good"? Are the evils of corporate rule really so blinding that dialectical materialism and monotheistic fundamentalism become indistinguishable?
"Commercial academicism" is more fundamental, right? Don't matter which party stands me up against the wall so's long it gets done. Well, fuck you, motherfucker.
Speaking of "sexual barbarism," and bearing in mind Badiou's argument that we shouldn't devalue the word "evil" by stretching it to cover totalitarianism and torture, I don't feel as guilty as I might about juxtaposing these excerpts:
"What does 'respect for the Other' mean when one is at war against an enemy, when one is brutally left by a woman for someone else...."
"Evil, then, ... is sexuality considered as merely a technique of pleasure."

Sadly, Bloomly, I can define good only as the opposite of evil. Good, like truth, is provisional and incomplete; evil, like deceit, is certain.
Is that liberal capitalism? So sue me. What do I look like, a philosopher over here?
But I do agree with the philosopher that calling everything "evil" all the time is a pretty annoying habit.
| . . . 2003-07-09 |
The Ultimate Rematch Between Good and Nice
I don't miss writing fiction. I do miss the workshops. Close reading has its limitations as a critical method, but no receiving transmitter could argue against its utility and pleasure.
Essays rarely get that level of attention, so I'm delighted that my Badiou tantrum elicited such an intelligent and extensive critique from Ezra Kilty.
Two lumps, please:
Which brings me to my tantrum's motive.
"Evil would be to compromise on the question of the Good." That is, the good is known and must remain unsullied. "Evil is the interruption of a truth." The truth is fixed and not to tampered with. "Evil is the destruction of a subject." Good subjects know their place. In Ezra's formulation, we should "honor and pursue whatever original conceptions we find ourselves having."
Fight the good fight for the good cause. The man can't bust our music.
But not all causes are equally certain goods, nor are all hypotheses, nor are all original conceptions, nor even is all music. In ethics, politics, science, and art, it's often better to let our cause be judged and influenced by the complexities and compromises that our efforts encounter and produce. By the trivial. By the mean.
Ezra doesn't mention Badiou's "four fundamental Evils," so I assume he wasn't as appalled as I was. Deceptions, torture, mass murder: Badiou calls them legitimate means to the Good, as all means are -- except for "obscurantism, commercial academicism, the politics of profit and inequality, and sexual barbarism." It doesn't matter what other benefits might be gained from those means: they're off limits. Only the vilest of humanity would take a paying academic job or partake of sexual pleasure.
But with those exceptions, to use our native homily, the end justifies the means.
Now while that's true for some ends and some means, it doesn't seem to me a universal truth. There may be more than one means to an end (I might grow a tomato to feed myself, or I might bash your skull and stick you in the deep-freeze). There may be more than one end. Means may conflict. The ends may be provisional.
All sophomoric enough, which is why you only hear certain types of post-sophomore say things like "The end justifies the means."
By that bit of wisdom those types usually mean "An extreme end justifies extreme means," with "extreme" a strangled recognition of moral repugnance: a shame which we preemptively deny.
And those types often seem, to me anyway, addicted to extremity. Their means are dwelt on; their supposed ends are comparatively unexamined, distant, and unlikely -- almost an afterthought -- plug-and-play. The viciously callow anarchist matures into the viciously callow Republican.
Then there's the problem of dealing with those who might profess different goals, god forbid. (Presumably they exist; presumably they're why our goal has not yet been achieved.) If one thinks of them as targets of deceit, torture, or murder, they're simply opportunities. But if one treats them as problematic? Well, that's the problem icky old liberal democracy was meant to solve -- by dealing-with rather than by elimination, admittedly and, to many powerful trend-setters, unacceptably. "Grandeur" may be unfashionable in Badiou's circle, but it's the little black dress of John Ashcroft's and Osama bin Laden's.
More mundanely, we have the heterosexual who despises all women (if divorced) or all women but his wife (if married). The libertarian dreaming of tax-free fiery glory. The daddy's-girl feminist who insults and exploits female workers. The tenured Marxist who bullies subordinates. The poet who sacrifices all within arm's reach to the manufacture of elegaic moods.
I know these people all too well -- from the inside out. I judge Badiou's judgment in my light, as I suppose he'd have me do.
A life spent ruining other lives for the sake of a fantasy so persistently distant that its flaws can't be detected -- I admit it's a catchy narrative. I refuse to concede that it's a good life.
| . . . 2003-11-24 |
Errata
Having had occasion to review my "bit of blog about Badiou," Adam Tobin rightly takes me to task:
While I have you on the line, I'd also like to say that (contrary to your claim that they are evil) soap operas are not single-POV heroic narratives, although such are often used as materials: Chris is pleased to learn that his private eye has already dug up some juicy dirt on his kid brother. Meanwhile, Livvie makes it clear to Jack how much she wants him to make love to her. A flustered Lucy asks Kevin how he can possibly think of leaving Port Charles now that he knows he has a daughter. Eve steps out of her bath to find Ian staring at her. When Harris returns to claim his "prize", Eve covers by assuring a worried Ian that she's only going out to explain the next medical procedure to their captor. Kevin is forced to bodily remove Lucy from the lighthouse but she stubbornly refuses to let go of his arm. Chris interrupts a moment of passion between Jack and Livvie.Honestly, I meant to refer only to the particular use made in a particular time and place of a particular convention of pseudo-realistic narrative: the division between protagonists (in the longest running soap operas of that time, the wise, good-hearted, mostly passive observers; in sports, the home team; in lives of the poets, the poets) and antagonists (the amoral, weak-willed, and active villains; the visitors; the girlfriends).
But given the treatment usually doled out to gendered genres, I should have been more careful. For all I know, such soap operas aren't even made anymore, and even when they were, their toxicity wouldn't have compared with The 700 Club or "The Short Happy Life of Francis Macomber". To makers and viewers of soap operas, I apologize.
Badiou, on the other hand, can go peddle his papers.
| . . . 2020-06-23 |
While the Nightmare of Personal History changes reels, let's all go to the lobby for a chat.
What I'd like to emphasize in my otherwise unremarkable story is its from-the-start separation of mathematics from ontology.
Clearly I was a needy little boy, craving emotional shelter and unable to distinguish it from intellectual certainty, maybe because both were too elusive to enable a contrast. Received notions of "math people" as arrogant icicles would then suggest I took solace from mathematics' irrefragability.
Instead, the prepubescent period in which I was most rigidly rationalistic, positivist, orthodox, and puritanical was the same period in which I was "bad at math," and the period in which I studied math most intently was one of increasing aestheticism, relativism, and depravity. They grew together like, say, the rose and the brier. And that mathematical parallel-track (a little action on the side) terminated as my empirical-pluralism reached full ripeness.
In Ian Hacking's Why Is There Philosophy of Mathematics at All?, his answers include a pair of mathematical pleasures peculiar enough to invite analysis:
1. Proofs
Logical demonstrations were indeed the means by which Miz Johnson transported me to a comfortable home in math, but that comfort was drawn from familiarity rather than novelty. She'd shown how mathematical study could be made to merge with my studies of fictional narrative, poetic form, and discursive rhetoric, all of which required similar reconstitutions of achronological higher-dimensional cognitive structures from chronologically sequenced discourse, and all of which rewarded me with a similarly stabilizing pleasure.
There's an obvious difference, of course. Outside mathematics, even something as seemingly straightforward as a location or a date could become contentious, and god help anyone who claims to establish causality. Subjective certainty is felt across all disciplines, but mathematicians could be unusually confident that anyone willing and able to follow their demonstration would feel the same subjective certainty.
Math doesn't just construct knowledge; it constructs objective knowledge: rational coherence creates objectivity; objectivity leads to new discoveries/inventions, which then provide properly air-dried fodder for rational coherence. And yes, there's something attractively restful about objectivity.
Equally, there's something agitating about construction — it's not all lunch breaks and wolf-whistling, you know. And if anything, what drew me to this newly-understood conception of mathematics was its brush-clearing exposure of the difference between objective knowledge and a conservative ontology of static being:1
This approach will obviously replace, in mathematics and in natural science, the notion of “ontological truth” by knowledge construction, the ultimate result of the human cognitive activity, as well as, thanks to this activity on reality, the notion of construction of objectivity.- Mathematics & the Natural Sciences by Giuseppe Longo & Daniel Bailey
We call a proposition "true," not because it agrees with a fixed reality beyond all thought and all possibility of thought, but because it is verified in the process of thought and leads to new and fruitful consequences.- Substance and Function by Ernst Cassirer
Now, it is not because a concept can be defined in set-theory that the concept makes sense. This is most flagrantly demonstrated for the concept of truth, defined by Tarski by means of a pleonasm, typically:∀x A[x] is true when A[n] is true for any integer n
The truth of A is nothing but A, which is what we called essentialism. One must legitimately doubt a notion that turns out to be so opaque. In place of the academistic interpretation « want of truth », I propose to substitute the more stimulating « truth means nothing » (I didn’t say « is not definable in arithmetic », I really meant « no meaning »). Which does not imply that I was wrong in saying that G is true, since we established it. I only say that, in the same way there is no general notion of beauty, good, etc., there is no « general » definition of truth. What we logicians manipulate under the name « true » is only an empty shell.
- The Blind Spot: Lectures on Logic by Jean-Yves Girard
At the same time, mathematics exposed the gulf between objectivity and experience. Although mathematics made some of its most startling advances by way of working around obstacles to material application, those were momentous interventions rather than day to day practice, and in the most obsessive-compulsive notion of "proofs," they have no place at all. The price of peace was a certain distancing from life.
And since life (rather than logic) was the source of my perplexity, this obvious difference was not entirely to math's advantage. For me, then, the chief pleasure of proof was not that aspect specific to mathematics.
Nor is it always present in mathematics, any more than the intuition of aesthetic structure depends upon having a verbal projection of that structure:
Jena, Feb. 8 1793Your idea of the dominating power is based on the idea of the whole, on the concept of the unity of the connected parts, the manifold, but how can we recognize this unity? Apparently only through a concept; one must have a concept of the whole under which the manifold is united. [...] Now, Kant is certainly right in saying that the beautiful pleases without a concept. I can have found an object beautiful for quite a while before I am able to articulate the unity of its manifold, and to determine what power dominates it.
- Friedrich Schiller, ‘Kallias or Concerning Beauty: Letters to Gottfried Körner’
translated by Stefan Bird-Pollan,
from Classic and Romantic German Aesthetics, ed. J. M. Bernstein
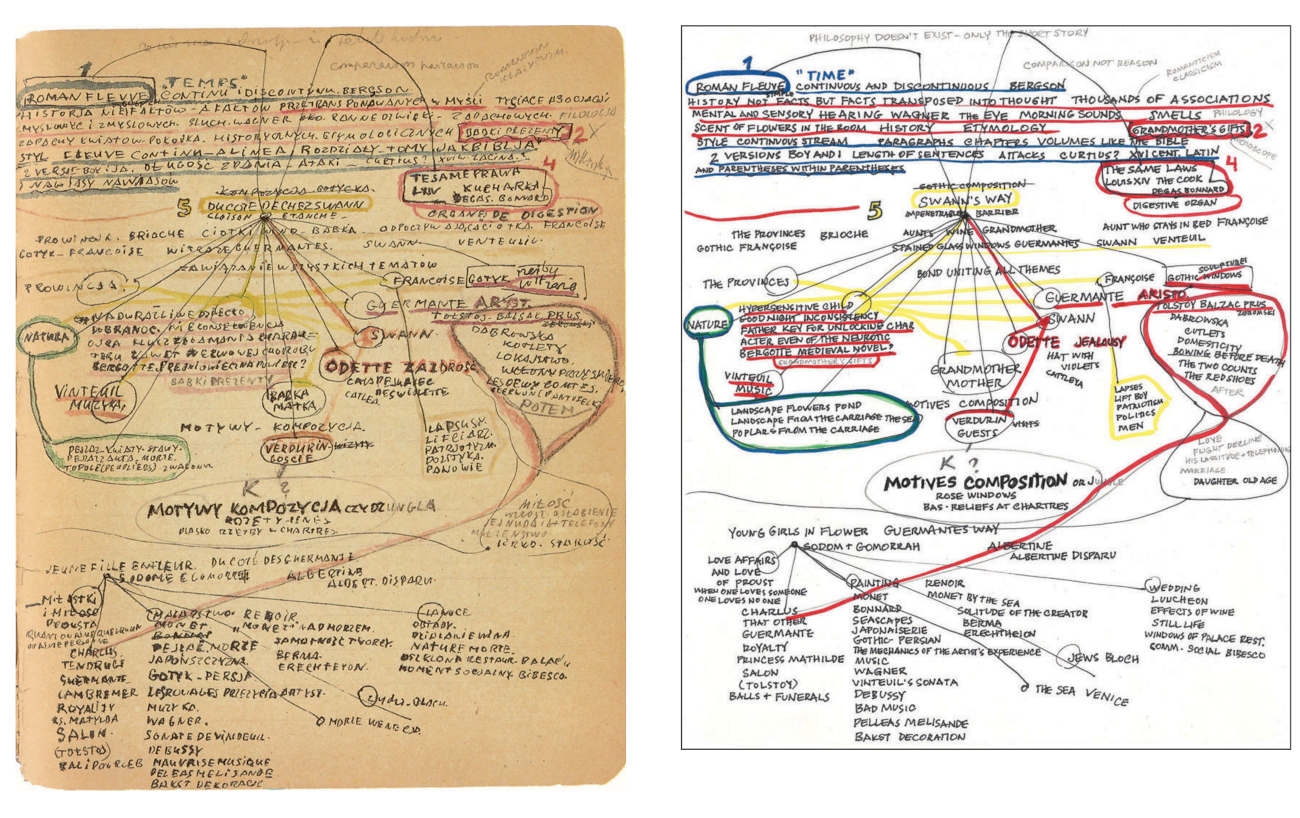 Józef Czapski carries an intuited manifold of À la recherche du temps perdu into prison camp... |
| and projects a slice onto sequential discourse.  |
Just as aesthetic objects and operations must be intuited before they can be analyzed, mathematical objects and operations must be intuited before being established by proof. And, as tediously demonstrated by pre-Miz-Johnson classes, mathematical objects can be (and mostly are) studied proof-free as off-the-shelf tools. Disputatious Greeks found a need to hybridize those tools with logical arguments, but not everyone does. "Calculus for Engineers" will always draw more students than "Category Theory for Philosophers." To quote Hacking citing someone else who isn't Chinese:
China, in ancient times, developed brilliant mathematics, but it chiefly worked on a system of approximations. Proof seems seldom to have reared its head in China, and was seldom esteemed in its own right. Geoffrey Lloyd, who has devoted his mature years to comparative Chinese/European intellectual history, notes that the hierarchical structure of a powerful education system, with the Emperor's civil service as the ultimate court of appeal, had no need of proofs to settle anything.
According to histories of Western mathematics, no intuited hypothesis, theorem, or equation is fully accepted by the discipline until it's been convincingly (objectively) proven. What strikes the reader of such histories, however, is how long the wait for that proof might be. Even after one is provided, skeptics may demand (or the ambitious may publish) clearer, more convincing proofs. And yet during that time the mathematical intuition remains part of "mathematics" and no other discipline, and may be put to use.
And professional surveys show that the proofs prized most by mathematicians were those whose techniques and transitional byproducts became productive in their own right. The best proofs aren't built for contemplative coziness but for leaving.
Which brings us to the second of Hacking's pair, the pleasure of transference — the unexpected applicability of an existing mathematical object in a new context — which he splits into its own sub-pair:
2.1. What Eugene Wigner called "The Unreasonable Effectiveness of Mathematics in the Natural Sciences."
2.2. What David Corfield called "the unreasonable effectiveness of mathematics in mathematics."
2.1. Transfers out of math
"All else being equal," two full-grown hogs are equivalent to two swimming pools. But the equality of these elses depends on hunger, heat, financial need, and so on. If we want a working pretext of arithmetical certainty, we'll need some third entity that can set a ratio with some wiggle room. And so as social groups grow (possibly by force), the lure of easily transported objectivity — arithmetical certainty — urges economies towards money or something like, but even Adam Smith knew that money economies needed constant intervention to maintain the objective fiction. (Ayn Rand was more a "Pi equals 3.0" sort of capitalist.)
Although the neighborhoods-of-Euclidean-space found in Riemann's continuous-manifold might be thought of as a formalization of "wiggle room," formality forbids much wiggling. Almost by definition mathematics consists of only and all "things being (objectively) equal" and anything outside mathematics is almost by definition not precisely equal. Mathematical objects are unambiguous non-conflicting abstractions drawn from the world, mathematics is the unambiguous non-conflicting rhetoric thereof, and so a match (with wiggle room) between mathematics and selected aspects of reality seems no more startling than effective real-life applications of fables, novels, aphorisms, plays, or jokes. The unreasonable correspondence of mathematics to the world is simply the exsanguinated and beetle-cleaned progeny of the unreasonable correspondence of words to the world.
2.2. Transfers within math
Like (in their incalculably better informed ways) Hacking, Winfried Scharlau, Gian-Carlo Rota, Giuseppe Longo, Fernando Zalamea, and Wittgenstein,2 in my doltish, shallow, smash-grab-and-run way I was impressed less by the ontological immortality of mathematical truth, or its commercial applicability, than by its cross-breeding variety-unity. Its entities merge and multiply like skeletonic goats and monkeys, and Pascal was right to condemn mathematics as another sin of the flesh. "Saint Francis didn't run numbers."
I should like to say: mathematics is a MOTLEY of techniques of proof.— And upon this is based its manifold applicability and its importance.- Remarks on the Foundations of Mathematics by Ludwig Wittgenstein,
third revised edition
I would like to advance the thesis that the decisive condition for the origin of pure mathematics was the fact that for the first time in the history of mathematics a large number of connections were discovered between seemingly different problem areas and results. Until well into the 18th century, mathematics was comprised of many isolated areas of study, into which some order was slowly introduced with the help of partially developed methods — for example differential equations and the calculus of variations in analysis. The range of application of these methods was easily grasped and apparently somewhat limited. Then connections between the most distant branches of mathematics suddenly appeared. It is obvious that this must have led to a completely new intensity of development and that this development rose to a new level. To that extent I maintain rather the opposite of Struik: Pure mathematics originated in the transcending of special viewpoints.- "The Origins of Pure Mathematics" by Winfried Scharlau
The back-and-forth between diverse perspectives (conceptual, hypothetical, deductive, experimental), diverse environments (arithmetical, algebraic, topological, geometrical, etc.) and diverse levels of stratification within each environment is one of the fundamental dynamic features of modern mathematics. [...] It was necessary, for example, for obstructions in infinitary systems of linear equations and in classes of integral equations to be confronted in order for the notion of a Hilbert space, one of modern mathematics' most incisive mixtures, to emerge, just as certain singularities in complex variable functions had to be confronted for another paradigmatically modern construction, the notion of Riemann surfaces, to emerge. Similarly, Galois theory — one of the great buttresses of mathematics' development, with remarkable conceptual transfers into the most varied mathematical domains — would be unthinkable had important obstructions between webs of notions associated with algebraic solutions and geometrical invariants not been taken into account. In order to tackle problematics of great complexity — stretched over highly ramified dialectical warps — modern mathematics finds itself obliged to combine multiple mathematical perspectives, instruments and bodies of knowledge.- Synthetic Philosophy of Contemporary Mathematics by Fernando Zalamea
The mystery as well as the glory of mathematics lie not so much in the fact that abstract theories do turn out to be useful in solving problems, but in that wonder of wonders, in the fact that a theory meant for one type of problem is often the only way of solving problems of entirely different kinds, problems for which the theory was not intended. These coincidences occur so frequently that they must belong to the essence of mathematics.- "The Concept of Mathematical Truth" by Gian-Carlo Rota
I'd say the histories of literature, of art, of music, of history, and so on exhibit at least as many motivational obstructions and liberating intradisciplinary transfers as the history of mathematics. Still, for me as well (if not as intelligently) as Rota, the pleasure of unexpected transference feels purest (and perhaps most essential) in mathematics, if only because mathematics is made of little else and its transfers tend to be met by relatively short-lived controversy. (Mathematicians save their most lasting rage for squabbles over personal credit. Subjectivity needs to assert itself somehow, I guess.)
But these magical entities gain their ubiquity, flexibility, and stability at the cost of — pretty much everything unmagical? Although the claim that mathematics consists of nothing but tautology is as silly as claiming that a dictionary replaces a library, it's transparently more self-sufficient than other disciplines. For all the impressive fecundity of mathematics' tangle of sturdy dead-oak, a glance over the hedge will show how bare the lawn of excluded middle really is.
The lights are dimming and so am I. Back to our seats; I hear his full-frontal scene's coming up.
1 None of the cited authorities were available to me at the time. In Missouri, foundations-and-philosophy of math stopped at Frege and Russell; in college, those foundations seemed increasingly superfluous, set-theorized reductionism seemed increasingly anorexic, and I gave up on systematic synthesis. More recent philosophers better match my own experience.
On the side of "a fixed reality beyond all thought," ontological proofs of God were always easy to find but just as easily discarded: the axiom that existence is undeniably a universal good struck me as more than questionable, the world did not (to my mind) much resemble a very expensive, very reliable, perpetually self-winding watch, and (just between us) the Jehovah of Job sounds a bit blustery.
2 Other than Wittgenstein, all these writers were influenced by post-WWII category theory, established as a central transit hub by Alexander Grothendieck, William Lawvere, and others, but as of the late 1970s still considered too advanced for undergraduates like myself. At my present-day rank of duffer, by far the best introduction I've found is by Lawvere in collaboration with Stephen Schanuel: Conceptual Mathematics: A First Introduction to Categories, a textbook which does for category theory what the New Math did for set theory.
Don't get me started on Badiou.
Copyright to contributed work and quoted correspondence remains with the original authors.
Public domain work remains in the public domain.
All other material: Copyright 2024 Ray Davis.